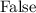The period T of a pendulum with length L is given by the formula:
![T=2\pi\cdot\sqrt[]{(L)/(g)}](https://img.qammunity.org/2023/formulas/physics/college/snzd42amdy85xf4xigj7t14spiu0tjn4hj.png)
Where g is the acceleration of gravity:
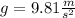
If the length of the pendulum is doubled, the period will be:
![\begin{gathered} T^(\prime)=2\pi\cdot\sqrt[]{(2L)/(g)} \\ =\sqrt[]{2}*2\pi\cdot\sqrt[]{(L)/(g)} \\ =\sqrt[]{2}* T \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/19h42g6sdr2r1qdhwkhttd7ivt77f5avy0.png)
On the other hand, the frequency is the reciprocal of the period. Then:
![\begin{gathered} f=(1)/(T) \\ f^(\prime)=(1)/(T^(\prime))=\frac{1}{\sqrt[]{2}* T}=\frac{1}{\sqrt[]{2}}*(1)/(T)=\frac{1}{\sqrt[]{2}}* f \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/jwfsstpwozy0noz1iw7yvi0kdw4n0oaq07.png)
Then, if the length of the pendulum is doubled, the frequency is cut by a factor of 1/√2:
![f^(\prime)=\frac{1}{\sqrt[]{2}}* f](https://img.qammunity.org/2023/formulas/physics/college/edi8pyqxawarj633feer5ddtyeu2pmy6i3.png)
This is not the same as if the frequency was cut by a factor of 1/2.
Therefore, the statement is: