Question

Find the solution of the system of equations.5 +2g = 185x-Y=36

Answer 1

Ok we have the following system of equations:

`\begin{gathered} 5x+2y=18 \\ 5x-y=36 \end{gathered}`

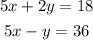
So the first thing to do is take one of the equations above and clear either x or y. I'm going to pick the second equation and clear y:

`\begin{gathered} 5x-y=36 \\ 5x=36+y \\ 5x-36=y \\ y=5x-36 \end{gathered}`

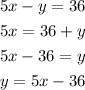
Now we substitute this result in the first equation:

`\begin{gathered} 5x+2y=5x+2\cdot(5x-36)=18 \\ 5x+10x-72=18 \\ 15x=18+72=90 \\ x=(90)/(15)=6 \end{gathered}`

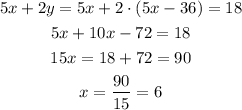
Now that we know x we take the result of clearing y from the second equation and find its value:

`\begin{gathered} y=5x-36 \\ y=5\cdot6-36=30-36 \\ y=-6 \end{gathered}`

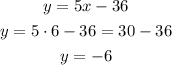
So in the end x=6 and y=-6.