1 Answer

Jijo John · Answer 1 · 2023-11-08T10:30:20+0000

Given exponential function:

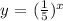
$y\text{ = (}(1)/(5))^x$

Let us obtain three points including the y-intercept so that we can plot the function y = f(x)

When x =0:

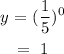
$\begin{gathered} y\text{ = (}(1)/(5))^0 \\ =\text{ 1} \end{gathered}$

when x =1:

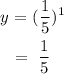
$\begin{gathered} y\text{ = (}(1)/(5))^1 \\ =\text{ }(1)/(5) \end{gathered}$

when x =2:

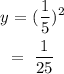
$\begin{gathered} y\text{ = (}(1)/(5))^2 \\ =\text{ }(1)/(25) \end{gathered}$

We have the points : (0, 1), (1, 1/5), and (2, 1/25)

Using these points, let us provide a sketch of the plot of y =f(x). We have the plot as shown below:

Please log in or register to add a comment.