Question

Fnd the volume of each cylinder below.9.18 in15 in

Answer 1

9) We can calculate the volume as the product of the base area and the height.

The base is a circle with radius r=18 in. Then, its area is:

`A_b=\pi r^2=\pi\cdot18^2=324\pi`

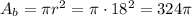
Then, we can calculate the volume V as:

`V=A_b\cdot h=324\pi\cdot15=4860\pi`

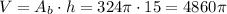
10) In this case the circular base is on the side, but we can still use the same principle to calculate the volume.

The area of the base with diameter D = 11 in is:

`A_b=(\pi D^2)/(4)=(\pi\cdot11^2)/(4)=(\pi\cdot121)/(4)=(121)/(4)\pi`

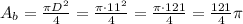
Then, we can calculate the volume V as:

`V=A_b\cdot h=(121)/(4)\pi\cdot21=(2541)/(4)\pi=635.25\pi`

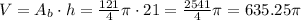
Answer:

9) V = 4860π

10) V = 635.25π