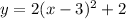1 Answer

Gijs Den Hollander · Answer 1 · 2023-03-08T23:07:30+0000

The function:

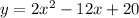
has the form:

with a = 2, b = -12, and c = 20.

The vertex form of a quadratic function is:

where (h,k) is the vertex.

The x-coordinate of the vertex, h, is computed as follows:

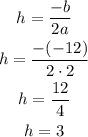
$\begin{gathered} h=(-b)/(2a) \\ h=(-(-12))/(2\cdot2) \\ h=(12)/(4) \\ h=3 \end{gathered}$

The y-coordinate of the vertex, k, is found replacing h into the formula of the function, as follows:

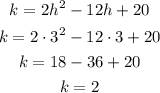
$\begin{gathered} k=2h^2-12h+20 \\ k=2\cdot3^2-12\cdot3+20 \\ k=18-36+20 \\ k=2 \end{gathered}$

Finally, the quadratic function in vertex form is:

Please log in or register to add a comment.