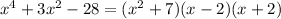Answer:
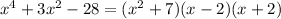
Explanation:
To factorize the expression, we can use a variable substitution. Let's say that z=x^2.
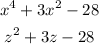
Then, to factorize this we need to factor in the form:
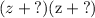
The numbers that go in the blanks, have to:
*Add together to get 3
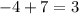
*Multiply together to get -28
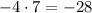
So, we get:
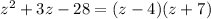
Substitute the equation z=x^2
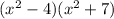
Factorizing the perfect square binomial: