The area of any shape after dilation is equal to the area of the original shape multiplied by the square of the scale factor:
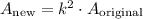
Where
A_new indicates the area of the shape after the dilation
A_original is the area of the original shape
k is the scale factor
The first step is to determine the area of the original shape and the new shape, using the formula:

The original shape has dimensions 4 and 5, so its area is:

Next is to determine the area of the shape after the dilation (A_new)
The scale factor is k=1.2
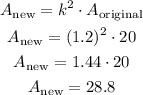
Now that we calculated both areas, we can determine the increase percentage.
- First, calculate the increase (I), which is the difference between the area of the new shape and the area of the original shape:
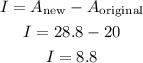
-Second, divide the increase by the original area and multiply the result by 100
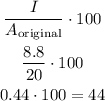
This means that the area increased 44% after the dilation