An equation is a mathematical expression that contains an equal sign. The objective of an equation is usually to determine the value of an unkown variable, commonly referred to x or y. In order to do that, however, we need to isolate the variable on the left side and this has to be done in a way that mantains the balance in the equation. This means that whatever operation we do on one side we have to perform the same exact operation on the other side. Let's take a look at an example.
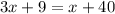
For this equation we have the unknown variable x, which is the value we want to find. Our goal is to isolate the variable on the left side, however we can see that there is one x on the right side, the first step will be to move this to the left side, this is what means to move the lowest variablem term first, because if we were to move "3x", which is the highest variable term, we would have to perform more steps to solve the equation.
To move the term "x" from the right to the left we need to subtract both sides by "x", this is because when we subtract "x-x" on the right side, the result will be 0 and we will be left with unkown variables only on the left. Let's check this out:
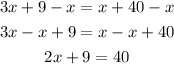
As we can see by doing so we eliminated the variable on the right side. Now we want to remove the 9 from the left side, we will have to perform a similar operation by subtracting 9 from both sides.
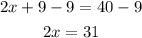
Now we have only a variable term on the left side, but it still being multiplied by 2 and we don't want that, so we have to divide both sides by 2.

With this we achieved the goal of the equation, which was to find the value of x. In short we always want to isolate the variable on the left side and to do that we will have to perform the inverse operation of the other terms in both sides of the equation, if a term is adding we need to subtract on both sides, if it is multiplying we need to divide on both sides and so on. We have to do that first with the term that contains the letter of lowest value, like we did with this one.