Question

25.10.2 Test (CST): Polynomial FunctionsQuestion 9 of 25Which of the two functions below has the smallest minimum .y-value?f(x) = x5-2g(x) = 3x² + 1O A. g(x)OB. There is not enough information to determineC. The y-values for f(x)and g(x) both go to -O D. f(x)SUBMIT

Answer 1

- To find the minimum values of the functions, we need to find the x-value of the vertex of the quadratic function, and then subsitute this x-value into the function to get its minimum value, while for the quintic equation, we simply apply the fact that it is an odd function. Because of this, the tails of the function move in opposite directions; one towards positive infinity, while the other moves towards negative infinity.

- The formula for finding the x-value of the vertex of a quadratic function is:

`x=-(b)/(2a),\text{ Given, }ax^2+bx+c=f(x)`

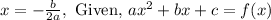
- Thus, we can find the x-value of the vertex for the quadratic equation as follows:

`\begin{gathered} f(x)=3x^2+1 \\ a=3,b=0,c=1 \\ \\ \therefore x=-(b)/(2a)=-(0)/(2(3))=0 \end{gathered}`

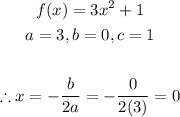
- Now that we have the x-value of the vertex of the quadratic equation, we can find its minimum value as follows:

`\begin{gathered} f(x)=3x^2+1 \\ put\text{ }x=0 \\ f(x)=3(0)^2+1 \\ f(x)=1 \end{gathered}`

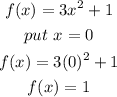
- Thus, the minimum value of the quadratic equation is 1.

- Next, we already know that the quintic equation moves down towards negative infinity. Thus f(x), the quintic equation, has a smaller minimum value

Final Answer

f(x), the quintic equation, has a smaller minimum value