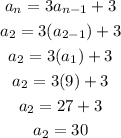Question

What are the first five terms of the recursive sequence aₙ = 3aₙ₋₁ + 3 where a₁ = 9

Answer 1

The expression for the recursive sequence is :

`a_n=3a_(n-1)+3`

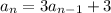
where a1 = 9

First term:

Since first term is already given:

`a_1=9`

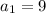
Second Term :

Substitute n =2 in the recursive expression and simlify

`\begin{gathered} a_n=3a_(n-1)+3 \\ a_2=3(a_(2-1))+3 \\ a_2=3(a_1)+3 \\ a_2=3(9)+3 \\ a_2=27+3 \\ a_2=30 \end{gathered}`

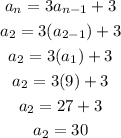
Second Term : 30

Third Term:

Substitute n = 3 in the given recursive expression:

`\begin{gathered} a_n=3a_(n-1)+3 \\ a_3=3(a_(3-1))+3 \\ a_3=3(a_2)+3 \\ a_3=3(30)+3 \\ a_3=90+3 \\ a_3=93 \end{gathered}`

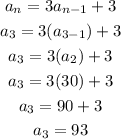
Third Term = 93

Fourth Term:

Substitute n = 4 in the given recursive expression:

`\begin{gathered} a_n=3a_(n-1)+3 \\ a_2=3(a_(2-1))+3 \\ a_2=3(a_1)+3 \\ a_2=3(9)+3 \\ a_2=27+3 \\ a_2=30 \end{gathered}`