The period of a tangent function y = atan(bx) is the distance between any two consecutive vertical asymptotes. And it is given by:
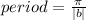
So, given the function y = tan x, we have that b = 1, therefore the period is:
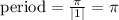
Next, between the given points:
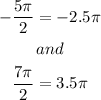
There are:
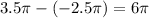
Since the period is π, so:
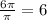
Answer: 6