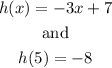Question

Find a linear function h, given h(3)=-2 and h(-3)=16. Then find h(5).

Answer 1

You have to find the equation of the linear function h(x), given that you know two points of the said function.

h(3)=-2 → this notation indicates the ordered pair (3,-2)

h(-3)=16 → this notation indicates the ordered pair (-3,16)

The first step to determine the equation of any line or linear function is to calculate its slope. To do so you have to use the following formula:

`m=(y_1-y_2)/(x_1-x_2)`

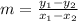
Where

(x₁,y₁) are the coordinates of one point of the line

(x,₂,y₂) are the coordinates of a second point of the line

Using the ordered pairs:

(3,-2) as (x₁,y₁)

(-3,16) as (x,₂,y₂)

Calculate the slope as follows:

`\begin{gathered} m=((-2)-16)/(3-(-3)) \\ m=(-18)/(3+3) \\ m=-(18)/(6) \\ m=-3 \end{gathered}`

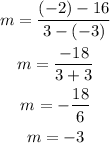
So the slope of the linear function is m=-3

To determine the equation you can use the point-slope form:

`y-y_1=m(x-x_1)`

Where

m represents the slope

(x₁,y₁) are the coordinates of one point of the line

I will use the point (3,-2) and the slope m=-3 to determine the equation but you can use either ordered pair to do so.

`\begin{gathered} y-(-2)=-3(x-3) \\ y+2=-3(x-3) \end{gathered}`

Now, what's left is to write the equation in slope-intercept form:

-Distribute the multiplication on the parentheses term:

`\begin{gathered} y+2=(-3)\cdot x-(-3)\cdot3 \\ y+2=-3x-(-9) \\ y+2=-3x+9 \end{gathered}`

-Pass "+2" to the right side of the equal sign by applying the opposite operation to both sides of the equal sign "-2"

`\begin{gathered} y+2-2=-3x+9-2 \\ y=-3x+7 \end{gathered}`

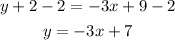
The equation of the linear function is:

`h(x)=-3x+7`

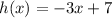
To find the value of h(5), you have to replace the equation of the function with x=5 and calculate the corresponding h(x) value

`\begin{gathered} h(x)=-3x+7 \\ h(5)=-3\cdot5+7 \\ h(5)=-15+7 \\ h(5)=-8 \end{gathered}`

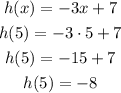
So:

`\begin{gathered} h(x)=-3x+7 \\ \text{and} \\ h(5)=-8 \end{gathered}`