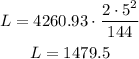Question

The safe load, L, of a wooden beam of width w, height h, and length l, supported at both ends, varies directly as the product of the width and the square of the height, and inversely as the length. A wooden beam 4 inches wide, 8 inches high, and 216 inches long can hold a load of 5050 pounds. What load would a beam 2 inches wide, 5 inches high, and 144 inches long, of the same material, support? Round your answer to the nearest integer if necessary.

Answer 1

We have the following, L, of the beam varies as the product of the width and the square of the height:

`L\propto w\cdot h^2`

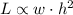
And varies inversely as the lenght of the wooden beam:

`L\propto(w\cdot h^2)/(l)`

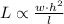
therefore:

`L=k\cdot(w\cdot h^2)/(l)`

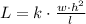
where k is the proportionality constant

w = 4, h=8, l = 216 and L = 5050

`\begin{gathered} 5050=k\cdot(4\cdot8^2)/(216) \\ k=(5050\cdot216)/(256) \\ k=4260.93 \end{gathered}`

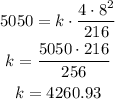
now, if w = 2, h = 5, l = 144:

`\begin{gathered} L=4260.93\cdot(2\cdot5^2)/(144) \\ L=1479.5 \end{gathered}`