1 Answer

Gianluca · Answer 1 · 2023-06-09T12:10:18+0000

Let us use the rule of the double of the angle

Since

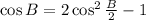
$\cos B=2\cos ^2(B)/(2)-1$

Substitute cos B by 7/8

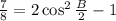
$(7)/(8)=2\cos ^2(B)/(2)-1$

Add 1 to both sides

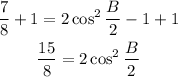
$\begin{gathered} (7)/(8)+1=2\cos ^2(B)/(2)-1+1 \\ (15)/(8)=2\cos ^2(B)/(2) \end{gathered}$

Divide both sides by 2

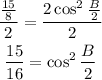
$\begin{gathered} ((15)/(8))/(2)=(2\cos ^2(B)/(2))/(2) \\ (15)/(16)=\cos ^2(B)/(2) \end{gathered}$

Take a square root for both sides

$\begin{gathered} \sqrt[]{(15)/(16)}=\cos (B)/(2) \\ \cos (B)/(2)=\frac{\sqrt[]{15}}{4} \end{gathered}$

let us find sin B

Since

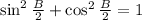
$\sin ^2(B)/(2)+\cos ^2(B)/(2)=1$

Then

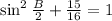
$\sin ^2(B)/(2)+(15)/(16)=1$

Subtract 15/16 from both sides

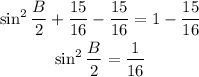
$\begin{gathered} \sin ^2(B)/(2)+(15)/(16)-(15)/(16)=1-(15)/(16) \\ \sin ^2(B)/(2)=(1)/(16) \end{gathered}$

Take a square root for both sides

$\begin{gathered} \sin (B)/(2)=\sqrt[]{(1)/(16)} \\ \sin (B)/(2)=(1)/(4) \end{gathered}$

Since

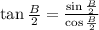
$\tan (B)/(2)=(\sin (B)/(2))/(\cos (B)/(2))$

Then

$\begin{gathered} \tan (B)/(2)=\frac{(1)/(4)}{\frac{\sqrt[]{15}}{4}} \\ \tan (B)/(2)=\frac{1}{\sqrt[]{15}} \end{gathered}$

The value of tan(1/2 B) is

$\frac{1}{\sqrt[]{15}}*\frac{\sqrt[]{15}}{\sqrt[]{15}}=\frac{\sqrt[]{15}}{15}$

Please log in or register to add a comment.