Question

Find the area of a triangle ABC when c = 15 m, a = 20 meters, and b = 10 meters.

Answer 1

Recall Heron's Formula to find the area of a triangle with sides a, b and c.

We define a new quantity s given by:

`s=(a+b+c)/(2)`

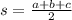
Then, the area of the triangle is given by the formula:

`A=√(s(s-a)(s-b)(s-c))`

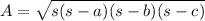
For a=20, b=10 and c=15 we have:

`s=(20+10+15)/(2)=22.5`

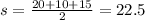
Then, the area of the triangle is:

`\begin{gathered} A=√(22.5(22.5-20)(22.5-10)(22.5-15)) \\ =√(22.5(2.5)(12.5)(7.5)) \\ =(75√(15))/(4) \\ =72.61843774... \\ \approx72.6 \end{gathered}`

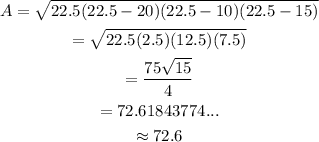
Therefore, the exact answer is:

`A=(75√(15))/(4)`

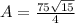
And the approximate area of the triangle ABC when c=15m, a=20m and b=10m is 72.6 m^2.