Question

A line passes through(1,-5) and (-3,7) write an equation for the line in point-slope form Rewrite the equation in slope-intercept form A. Y-5=1/3(x+1) ; y =1/3x + 16/3 B. Y+5=-3(x-1); y=-3x-2 C. Y-1=1/3(x+5);y=-1/3x+3/8 D. Y-5=3(x-1);y=3x+8

Answer 1

Step 1: Concept

Write the formula for the equation of a line in terms of point-slope form

and in slope-intercept form.

`\begin{gathered} Pi\text{ont slope form is given below} \\ y-y_1=m(x-x_1) \\ \text{Slope}-\text{intercept form} \\ y\text{ = mx + c} \\ m\text{ = }(y_2-y_1)/(x_2-x_1) \\ \end{gathered}`

Where

m = slope

c = intercept

Step 2: Represent the coordinates

`\begin{gathered} (x_1,y_1\text{ ) = (1, -5)} \\ (x_2,y_2\text{ ) = ( -3, 7)} \end{gathered}`

Step 3: Find the slope, using slope formula.

`\begin{gathered} m\text{ = slope} \\ \text{m = }(y_2-y_1)/(x_2-x_1) \\ m\text{ = }\frac{7\text{ -(-5)}}{-3\text{ -1}} \\ m\text{ = }\frac{7\text{ + 5}}{-4} \\ m\text{ = }(12)/(-4) \\ m\text{ = -3} \end{gathered}`

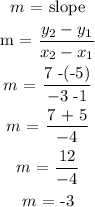
Step 4: Write an equation for the line in point-slope form.

`\begin{gathered} \text{y - y}_1=m(x-x_1) \\ y\text{ -(-5) = -3(x - 1)} \\ \text{y + 5 = -3(x - 1)} \end{gathered}`

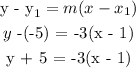
Step 5: Simplify the equation in 4 to write the equation in slope-intercept form.

y + 5 = -3(x - 1)

y + 5 = -3x + 3

y = -3x + 3 - 5

y = -3x - 2

Final answer

Option B

y + 5 = -3(x - 1)

y = -3x - 2