Question

3) Select all ratios that are equivalent to 4:5 A. 2: 2.5 B. 2:3 C. 3: 3.75 D. 7:8 E. 8:10 F. 14: 27.5

Answer 1

For two ratios to be equivalent, its means and extremes if multiplied must be equal to each other.

`\begin{gathered} (a)/(b)=(c)/(d) \\ ad=bc \end{gathered}`

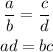
Let's start with Option A.

`\begin{gathered} (4)/(5)=(2)/(2.5) \\ 4*2.5=2*5 \\ 10=10 \end{gathered}`

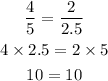
Since they are equal, then Option A is equivalent to 4/5.

Let's check Option B.

`\begin{gathered} (4)/(5)=(2)/(3) \\ 4*3=2*5 \\ 12\\e10 \end{gathered}`

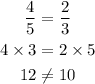
Let's check Option C.

`\begin{gathered} (4)/(5)=(3)/(3.75) \\ 4*3.75=5*3 \\ 15=15 \end{gathered}`

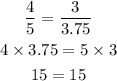
Let's check Option D.

`\begin{gathered} (4)/(5)=(7)/(8) \\ 4*8=5*7 \\ 32\\e35 \end{gathered}`

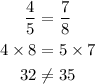
Let's check Option E.

`\begin{gathered} (4)/(5)=(8)/(10) \\ 4*10=5*8 \\ 40=40 \end{gathered}`

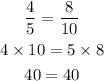
FInally, let's check Option F.

`\begin{gathered} (4)/(5)=(14)/(27.5) \\ 4*27.5=5*14 \\ 110\\e70 \end{gathered}`

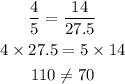
Hence, only Option A, Option C, and Option E are equivalent to ratio 4/5.