Question

What are the next 4 terms of the sequence 1, 6, 11...?

Answer 1

The formula to find the sequence is given by:

`a_n=a_1+(n-1)d`

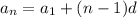
Where a1 is the first term of the sequence, n is the number of terms and d is the common difference. We can find the common difference by the following formula:

`d=a_n-a_(n-1)`

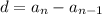
With the given terms of the sequence we can find d:

`\begin{gathered} d=11-6=5 \\ or \\ d=6-1=5 \end{gathered}`

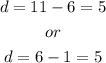
The common difference is d=5.

Now, apply the formual to find the next 4 terms of the sequence:

`\begin{gathered} a_4=1+(4-1)\cdot5=1+3\cdot5=1+15=16 \\ a_5=1+(5-1)\cdot5=1+4\cdot5=1+20=21 \\ a_6=1+(6-1)\cdot5=1+5\cdot5=1+25=26 \\ a_7=1+(7-1)\cdot5=1+6\cdot5=1+30=31 \end{gathered}`

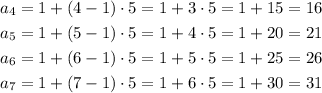
The next 4 terms are: A. 16,21,26,31