The bag contains,
Red (R) marbles is 9, Green (G) marbles is 7 and Blue (B) marbles is 4,
Total marbles (possible outcome) is,
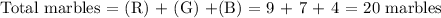
Let P(R) represent the probablity of picking a red marble,
P(G) represent the probability of picking a green marble and,
P(B) represent the probability of picking a blue marble.
Probability , P, is,
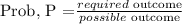

Probablity of drawing a Red marble (R) and then a blue marble (B) without being replaced,
That means once a marble is drawn, the total marbles (possible outcome) reduces as well,

Hence, the best option is G.