Question

The surface area of a rectangular prism is 60. Which of the following are possible dimensions of the rectangular prism? 1 Pt

Answer 1

The surface area of a rectangular prism with sides a, b and c is given by the formula:

`S=2(ab+ac+bc)`

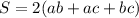
Use that formula to find the surface area that a prism with the given dimensions on each option would have.

A. 6, 2, 1 1/2

`\begin{gathered} S=2(6\cdot2+6\cdot1(1)/(2)+2\cdot1(1)/(2)) \\ =2(12+9+3) \\ =2(24) \\ =48 \end{gathered}`

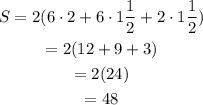
B. 5, 4, 1 1/4

`\begin{gathered} S=2(5\cdot4+5\cdot1(1)/(4)+4\cdot1(1)/(4)) \\ =2(20+(25)/(4)+5) \\ =2((125)/(4)) \\ =(125)/(2) \\ =62.5 \end{gathered}`

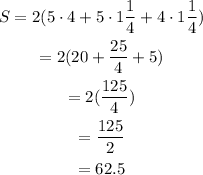
C. 3, 4, 1 1/2

`\begin{gathered} S=2(3\cdot4+3\cdot1(1)/(2)+4\cdot1(1)/(2)) \\ =2(12+3(3)/(2)+6) \\ =2(21(3)/(2)) \\ =45 \end{gathered}`

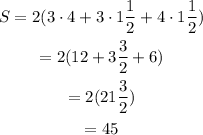
D. 6, 3, 1 1/3

`\begin{gathered} S=2(6\cdot3+6\cdot1(1)/(3)+3\cdot1(1)/(3)) \\ =2(18+8+4) \\ =2(30) \\ =60 \end{gathered}`

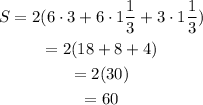
Therefore, the only possible dimensions of a rectangular prism with surface area 60 listed on the options, are 6, 3 and 3 1/3. The answer is:

`\text{Option D}`