Answer:
At least 16 service technicians
Explanation:
Given
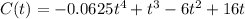
Required
Number of service technician to be online at 12 noon
First, we calculate the value of t
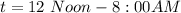
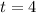
Substitute
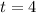 in
in
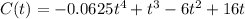
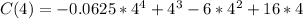
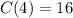
This implies that there are 16 customers online at 12 noon.
If 16 customers are online, then there should be at least 16 service technicians online.