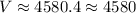Question

Find the surface area and volume of the figure .The surface area is _ft2.(Round to the nearest tenth as needed .)

Answer 1

Question:

Find the surface area and volume of the figure.

Solution:

1) The surface area:

This shape is composed of a cylinder and hemisphere. Now, we know that the surface area of the sphere is:

`SA\text{ sphere = 4}\pi\text{ }r^2`

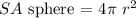
So that, the surface area of the hemisphere would be:

`SA\text{ hemisphere = }2\pi r^2`

On the other hand, the area of the circle is:

`A\text{= }\pi r^2`

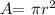
thus, the surface area of the cylinder would be:

`SA\text{ cylinder = }2\pi rh`

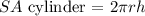
replacing the data given in the problem in the formulas of the surface area of the hemisphere, area of the circle, and surface area of the cylinder, we get:

`SA\text{ hemisphere = }2\pi(9)^2\text{ = 162}\pi`

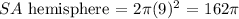
and

`SA\text{ cylinder = }2\pi(9)(12)\text{ = }216\pi`

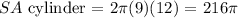
and

`A\text{= }\pi(9)^2=\text{ 81}\pi`

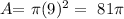
then, we can conclude that the surface area of the given figure is:

`SA\text{ = 162}\pi\text{ + 216}\pi+81\pi\text{ = 459}\pi\approx1441.9\text{ }\approx1442`

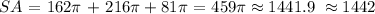
that is:

`SA\text{ }\approx1441.9\text{ }\approx1442`

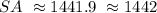
2) The volume

The volume of a cylinder is given by the following formula:

`V_C=\pi r^2h`

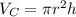
and the volume of a hemisphere is :

`V_H=(1)/(2)((4)/(3)\pi r^3)\text{ = }(2)/(3)\pi r^3`

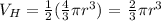
thus, the volume of the figure would be:

`V=V_C+V_H=\text{ }\pi r^2h\text{+}(2)/(3)\pi r^3`

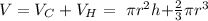
Then replacing the data given in the problem in the above formula we get:

`V=\pi(9)^2(12)\text{+}(2)/(3)\pi(9)^3\text{ = 972}\pi\text{+486}\pi=\text{ 1458}\pi\approx4580.4\approx4580`

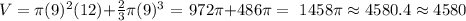
that is;

`V\approx4580.4\approx4580`