Question

Which of the following X-Y tables agrees withthe information in this problem?A puck moves 2.35 m/s in a -22.0° direction. A hockeystick pushes it for 0.215 s, changing its velocity to 6.42m/s in a 50.0° direction. What was the acceleration?A)хYYYC)хV 0.8802.18-0.8802.35-2.18ViVE4.134.92B)XVi2.35VE6.42a?Ax 0.2156.42> > 04.924.13a???Ax0.215ΔΧ??t0.2150.215tt 0.2150.215H

Answer 1

let's find the components for the initial velocity

`v_ix=2.35\cdot\cos (-22)=2.18`
`v_iy=2.35\cdot\sin (-22)=-0.88_{}`

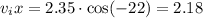
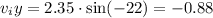
then for the final velocity

`v_fx=6.42\cdot\cos (50)=4.13`
`v_fy=6.42\cdot\sin (50)=4.92`

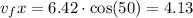
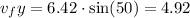
The table that agrees with the problem is A)

Then for the acceleration, we will use the next formula

`a=\frac{v_f-v_i_{}}{t}`

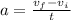
for the acceleration in x

`a_x=(v_fx-v_ix)/(t)=(4.13-2.18)/(0.215)=9.06m/s^2`

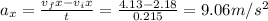
then for the acceleration in y

`a_y=(v_fy-v_iy)/(t)=(4.92-(-0.88))/(0.215)=26.97m/s^2`

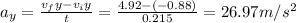
then we calculate the magnitude

`a=\sqrt[]{9.06^2+26.97^2}=28.45\text{ m/s}^2`