Question

A 6.25-gram bullet travelling at 365 m/s strikes and enters a 4.50-kg crate. The crate slides 0.15 m along a wood floor until it comes to rest.1. Find the friction force between the crate and the floor.

Answer 1

In order to determine the friction force, proceed as follow:

Take into account that total momentum of the system must conserve, then, you have:

m*v = (m + M)v'

where,

m: mass of the bullet = 6.25g = 0.00625kg

v: initial speed of the bullet = 365m/s

M: mass of the crate = 4.50kg

v': speed of both crate and bullet after the impact = ?

Solve the equation above for v', replace tha values of the other parameters and simplify:

Now, consider that the work done by the friction force is given by:

W = Fr*d

where,

Fr: friction force = ?

d: distance = 0.15m

Furthermore, the work done is equal to:

W = 1/2*(m+M)v'^2 that is, the change in kinetic energy is equal to the work

Then, you can equal the previous expressions for W, solve for Fr, replace and simplify:

`\begin{gathered} F_rd=(1)/(2)(m+M)v^(\prime)^2 \\ F_r=(1)/(2)((m+M)v^(\prime2))/(d) \\ F_r=(1)/(2)((0.00625kg+4.50kg)(0.506(m)/(s))^2)/(0.15m) \\ F_r\approx3.846N \end{gathered}`

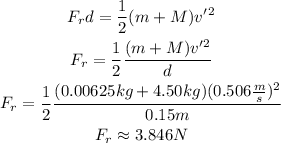
Now, take into account that the friction force can be written as follow:

Fr = μN = μ(m+M)g

where,

μ: coefficient of kinetic friction between crate and floor

g: gravitational acceleration constant = 9.8m/s^2

Solve the equatio above for μ, replace the values of the other parameters and simplify:

`\begin{gathered} \mu=(F_r)/((m+M)g) \\ \mu=(3.846N)/((0.00625kg+4.50kg)(9.8(m)/(s^2))) \\ \mu\approx0.087 \end{gathered}`

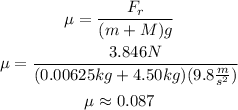
Hence, the coefficient of kinetic friction is approximately 0.087