Question

What effect does changing the function f(x)=3sin(x)+1to the function g(x)=3sin(x4)+2 have on the graph of f(x)?

Answer 1

Step 1

The parent function f(x) is given as;

`f(x)=3\sin (x)+1`

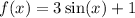
If we transform the function by adding 1 to it we will have;

`\begin{gathered} f(x)=3\sin (x)+1+1 \\ f(x)=3\sin (x)+2 \end{gathered}`

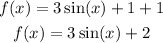
We have the following graph;

which means when you add 1 to the to get f(x)=3sin(x)+2, the function is shifted up by 1 unit.

Step 2

If the function is further transformed to;

`f(x)=3\sin ((x)/(4))+1`

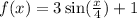
we will have the graph below;

This means that the graph stretches horizontally by a factor of 4.

Therefore the changes f(x) passes through to g(x) are;

`\begin{gathered} f(x)=2\sin ((x)/(4))+1_{}--(A\text{ horizontal stretch by a factor of 4)} \\ g(x)=2\sin ((x)/(4))+2---(A\text{ shift up by 1 unit)} \end{gathered}`

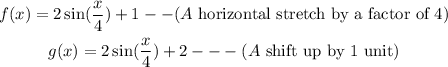
Answer; The graph is stretched horizontally by a factor of 4 and shifted up by 1 unit.