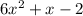SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the formula for area of a rectangle
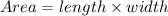
STEP 2: Write the given measure of the sides
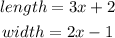
STEP 3: Calculate the area
By substitution,
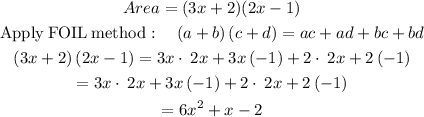
Hence, the area of the rectangle is