Question

What is the solution to the inequality 2-2x > -20

Answer 1

To determine the solution for the given inequality, you have to solve it for x:

`2-2x>-20`

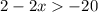
First, pass 2 to the right side of the inequality by applying the opposite operation to both sides of it:

`\begin{gathered} 2-2-2x>-20-2 \\ -2x>-22 \end{gathered}`

Next, note that the x-term is multiplied by "-2", to reach the value of x you have to cancel the said multiplication. For this, you have to divide both sides of the expression by "-2"

Now, keep in mind, that when you divide or multiply an inequality by a negative number, the direction of the inequality gets inversed. This means that the symbol "greater than, >" will tur into the symbol "less than. <":

`\begin{gathered} -(2x)/(-2)<-(22)/(-2) \\ x<11 \end{gathered}`

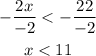
The solution for this inequality will be the values of x less than 11, symbolically: x < 11