Question

Fill in the blanks (B1, B2, B3) in the equation based on the graph.(a-B1)2 + (y-B2)² = (B3)²8182=83=Blank 1:

Answer 1

Given: a circle is given with center (3,-3) and equation

`(x-B_1)^2+(y-B_2)^2=(B_3)^2`

Find:

`B_{1,\text{ }}B_(2,)B_3`

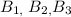
Step-by-step explanation: the general equation of the circle with center (a,b) and radius r is

`(x-a)^2+(y-b)^2=r^2`

in the given figure the center of the circle is at (3,-3)

so the equatio of the circle becomes

`(x-3)^2+(y+3)^2=(3)^2`

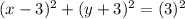
on comparing eith the given equation we get

`B_1=3,\text{ B}_2=-3\text{ and B}_3=3`