ANSWER
The interest rate is 150%
Step-by-step explanation:
Given that;
The initial amount is $5000
The total amount $20, 000 after 2 years
Total period of the investment is 2 years
To find the interest rate, follow the steps below
1. Find the interest on the investment after two years
In the given data,
The initial amount (principal) is $5000
The total amount after 2 years is $20, 000
Recall that,
Total amount = Interest + principal
20, 000 = interest + 5000
subtract 5000 from both sides of the equation
20, 000 - 5,000 = interest + 5000 - 5000
15,000 = interest
Therefore, the interest on the investment after 2 years is $15, 000
Step 2; Find the interest rate using the simple interest formula
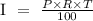
Where
I is the interest
P is the principal
R is the interest rate
T is the time of the investment

Therefore, the interest rate is 150%