If a parallelogram PQRS has diagonals PR and SQ that intersects at T, then, T is the midpoint of PR and T is the midpoint of SQ
Given
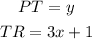
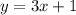
Also
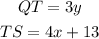
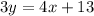
Now we are going to solve the system of equations with two unknowns

Substitute equation 1 into 2
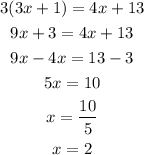
x = 2
Substitute x = 2 into equation 1
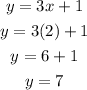
y = 7
The answer would be x = 2, y = 7