Since he has 15 vessels and needs to choose 5, we can use a combination of 15 choose 5 to calculate the number of possible ways, since the order of the vessels inside the group of 5 is not important.
The formula to calculate a combination of n choose p is:
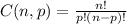
Then, for n = 15 and p = 5, we have:

So there are 3003 ways to choose the 5 vessels.