Given:
there are two types of tickets to a show: advance and same-day
Let the number of tickets from the type of Advance = x
And the number of tickets from the type of Same-day = y
there were 50 tickets sold in all
So,
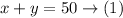
Advance tickets cost $30 and same-day tickets cost $15.
the total amount paid for them was $1275
So,
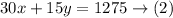
Solve the equations (1) and (2) to find (x) and (y)

So, The answer will be:
The number of tickets from the type of Advance = x = 35
And the number of tickets from the type of Same-day = y = 15