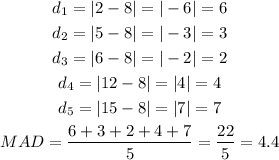Question

What is the mean absolute deviation (MAD) of the dada set? 2, 5, 6, 12, 15 Enter your answer as a decimal in the box.

Answer 1

To get the mean absolute deviation, we first need the mean of the set. The mean is calculated by the sum of the values divided by the number of data:

`\begin{gathered} \mu=(2+5+6+12+15)/(5) \\ \mu=(40)/(5) \\ \mu=8 \end{gathered}`

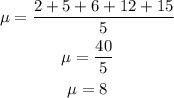
To get the means absolute deviation, we have to get the absolute difference between each data and the mean, sum them up and divide by the number of data:

`\begin{gathered} d_1=|2-8|=|-6|=6 \\ d_2=|5-8|=|-3|=3 \\ d_3=|6-8|=|-2|=2 \\ d_4=|12-8|=|4|=4 \\ d_5=|15-8|=|7|=7 \\ MAD=(6+3+2+4+7)/(5)=(22)/(5)=4.4 \end{gathered}`