Question

Can you please write the basic equation forConstant parent functionInverse sine parent functionInverse cosine parent function Inverse tangent parent function

Answer 1

• In order to understand this, we need to know that an inverse trigonometric function “undo” what the original trigonometric function

• e.g Trig function : inverse of trig. function .

Explanations :

(a) Inverse sine parent function:

The inverse y = six x parent function will be

`\begin{gathered} y=sinx^(-1)\text{ ; meaning } \\ x\text{ = sin y } \end{gathered}`

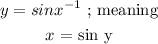
• y = sinx ^-1 , has domain at [-1;1] and range at (-/2; /2)

(b)Inverse cosine parent function

the inverse of y = cos x parent function will be :

`\begin{gathered} y=cosx^(-1);\text{ meaning } \\ x\text{ = cos y } \end{gathered}`

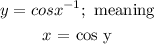
• y = cosx^-1 , has domain at [-1;1] and range at (0;)

(c)Inverse tangent parent function

The inverse of y = tan x parent function will be :

`\begin{gathered} y=tanx^{-1\text{ }},\text{ meaning } \\ x\text{ = tan y } \end{gathered}`

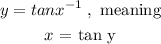
• y = tanx^-1 has domain at (-∞;∞) and range at (- /2 ; /2)

see the graphs below that shows the asympotes of the trigonometric function.