Question

Here are the graphs of three equations:y = 50(1.5) ^xy = 50(2)^xY = 50(2. 5)^xWhich equation matches each graph? Explain how you know

Answer 1

The graphs below are exponential function graphs, the general formular takes the form

`y=ab^x`

The graph of

`y=50(1.5)^x`

Is shown below

The graph of

`y=50(2^x)`

Is shown below

The graph of

`y=50(2.5^x)`

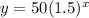
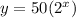
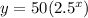
Is shown below

Hence,

`\begin{gathered} y=50(1.5)^x\rightarrow C \\ y=50(2)^x\rightarrow B \\ y=50(2.5)^x\rightarrow A \end{gathered}`

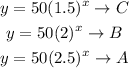
The equation of the exponential function is

`\begin{gathered} y=ab^x \\ a=50\rightarrow the\text{ initial value} \\ b\rightarrow growht\text{ factor} \end{gathered}`

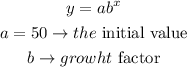
Thus the higher the growth factor the greater the rate of attaining a higher value within a short period.

That is why you see that the function with growth factor of 2.5 grows faster than that of 2 and also 1.5.

So the at x value of 3, the function with the greatest growth factor will have the highest y-value.

This implies , growth factor of 2.5 will have the highest, that corresponds to graph with colour green. Function with growth factor 2 will be the next to that of 2.5, that is red colored graph, and the last will be blue.