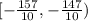Question

May I please get help with Solve for x: −3<−10(x+15)≤7

Answer 1

Given the compound inequality;

`-3<-10(x+15)\le7`

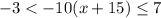
We would begin by simplifying the parenthesis as follows;

`\begin{gathered} -3<-10(x+15) \\ \text{AND} \\ -10(x+15)\le7 \end{gathered}`

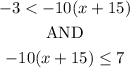
We shall now solve each part one after the other;

`\begin{gathered} -3<-10(x+15) \\ -3<-10x-150 \\ \text{Collect all like terms and we'll have;} \\ -3+150<-10x \\ 147<-10x \\ \text{Divide both sides by -10} \\ (-147)/(10)>x \end{gathered}`

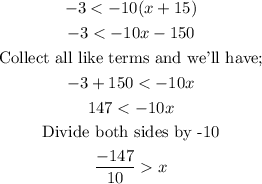
We can switch sides, and in that case the inequality sign would also "flip" over, as shown below;

`\begin{gathered} (-147)/(10)>x \\ \text{Now becomes;} \\ x<(-147)/(10) \end{gathered}`

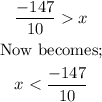
For the other part of the compound inequality;

`\begin{gathered} -10(x+15)\le7 \\ -10x-150\le7 \\ \text{Collect all like terms and we'll have;} \\ -10x\le7+150 \\ -10x\le157 \\ \text{Divide both sides by -10} \\ (-10x)/(-10)\le(157)/(-10) \\ x\ge-(157)/(10) \end{gathered}`

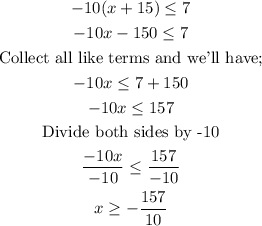
Therefore, the values are;

`\begin{gathered} x<-(147)/(10) \\ \text{And } \\ x\ge-(157)/(10) \\ \text{Hence;} \\ -(157)/(10)\le x<-(147)/(10) \end{gathered}`

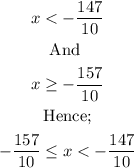
Written in interval notation, this now becomes;

`\lbrack-(157)/(10),-(147)/(10))`