Question

How to graph inequalities y + 6 < 10 or 2y - 3 > 9

Answer 1

We need to graph on the number line the solution to the compounded inequality

`\begin{gathered} y+6<10 \\ \text{or } \\ 2y-3>9 \end{gathered}`

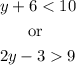
In order to do so, let's work with each inequality separately. The final solution will be the union of the two solutions since it can be one "or" the other.

Step 1

Subtract 6 from both sides of the first inequality:

`\begin{gathered} y+6<10 \\ \\ y+6-6<10-6 \\ \\ y<4 \end{gathered}`

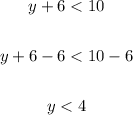
So, the solution to the first inequality is all real numbers less than 4 (not included). Therefore, we graph this solution using an empty circle:

Step 2

Add 3 to both sides of the second inequality, and then divide both sides by 2:

`\begin{gathered} 2y-3+3>9+3 \\ \\ 2y>12 \\ \\ (2y)/(2)>(12)/(2) \\ \\ y>6 \end{gathered}`

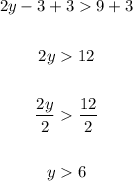
Thus, the solution to this inequality is all the real numbers greater than 6 (not included: empty circle):

Answer

Therefore, the solution to the compounded inequalities is the union of both solutions: