Given:
Given the system of equations:
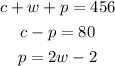
Required: Solution of the system using Cramer's rule
Step-by-step explanation:
The system of equations can be rewritten as
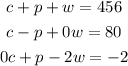
Write down the augmented matrix.
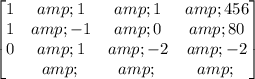
Calculate the main determinant.
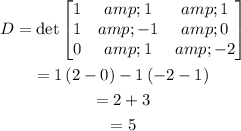
Substitute the c-column with RHS and find the determinant.
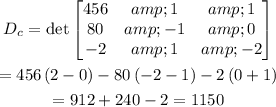
Substitute the p-column with RHS and find the determinant.
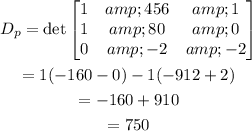
Substitute the w-column with RHS and find the determinant.
![undefined]()