Now for the point A), L is in the middle of M and H, and the interval will be:
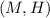
For the second point, We need to put the value of the segments in the draw...
From the draw, we can deduce that:
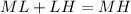
We replace with values:
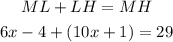
We solve to x:
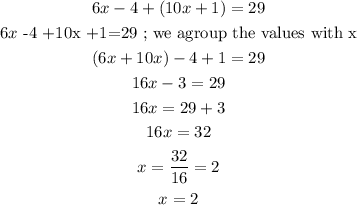
Finally, if the value of x = 2, then whi can replace in:
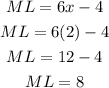
Your answer of point B) is ML=8.