Question

For the following set of data, find the number of data within 1 population standarddeviation of the mean.68, 68, 70, 61, 67, 71, 63, 67

Answer 1

Given the following set of numbers,

`68,\text{ 68, 70, 61, 67, 71, 63, 67}`

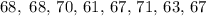
Where the (n) number of data is 8, the mean is,

`\bar{x}=\frac{x_1+x_2+..._{}+x_n}{n}=(68+68+70+61+67+71+63+67)/(8)=66.875`

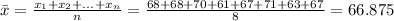
The standard deviation is 3.36

Hence, the interval that is 1 population within the mean is given by

`(66.88-3.36,66.88+3.36)=(63.52,70.24)`

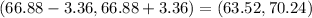
Of all the data only 71, 61, and 63 are not an element of the interval (63.52,70.24)

The total number of data is 8.

Hence, the total number of data within 1 standard deviation of the mean is 5