Given data:
Area of plates:
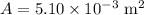
Separation between the plates:
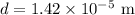
Potential difference:
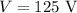
The capacitance of the capacitor is given as,
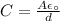
Here, ε_o is the permittivity of the free space.
Substituting all known values,
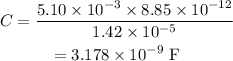
The charge on the capacitor is given as,
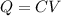
Substituting all known values,
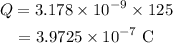
Therefore, the charge on the plates is 3.9725×10^-7 C.