Question

Near the top of the Citigroup Center building in New York City, there is an object with mass of 4.00 ✕ 105 kg on springs that have adjustable force constants. Its function is to dampen wind-driven oscillations of the building by oscillating at the same frequency as the building is being driven—the driving force is transferred to the object, which oscillates instead of the entire building.(a) What effective force constant (in N/m) should the springs have to make the object oscillate with a period of 2.10 s? N/m(b) What energy (in J) is stored in the springs for a 1.80 m displacement from equilibrium? J

Answer 1

ANSWERS

(a) 3.58 x 10⁶ N/m

(b) 5.8 x 10⁶ J

Step-by-step explanation

Given:

• The mass of the object hanging from the spring, m = 4.00 x 10⁵ kg

Find:

• (a), The force constant the springs should have to make the object oscillate with a period of 2.10 s

,

• (b), The energy stored in the springs for a 1.80 m displacement from equilibrium.

(a) The period of an object in a spring is,

`T=2\pi\sqrt{(m)/(k)}`

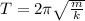
Where m is the mass of the object and k is the spring constant.

We want to find k for T = 2.10 s, so we have to solve this equation for k, which gives us,

`k=m\cdot\left((2\pi)/(T)\right)^2`

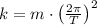
Replace the known values and solve,

Hence, the force constant is 3.58 x 10⁶ N/m.

(b) The energy stored in a spring with force constant k when the mass is displaced x meters from equilibrium is,

`U_s=(1)/(2)kx^2`

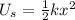
Replace the known values and solve to find the energy stored in this spring,

`U_s=(1)/(2)\cdot3.58\cdot10^6N/m\cdot1.8^2m^2\approx5.8\cdot10^6J`

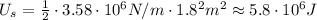
Hence, the energy stored in the spring for a 1.80 m displacement from equilibrium is 5.8 x 10⁶ J.