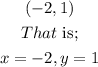Step-by-step explanation:
We are given the linear equation;
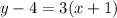
To graph this equation, we would begin by re-writing the equation in the slope-intercept form, which is;

To do this, we first expand the parenthesis;
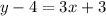
Next we add 4 to both sides;
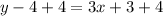
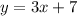
We can now begin to plot the various points on the line. Starting from, x = -2 we would have;
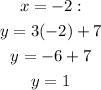
We can now go on and plot other points depending on the limit imposed by the graph page.
However, what we have here shows the coordinates from which we may begin;
ANSWER: