Answer:
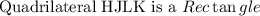
Step-by-step explanation:
Here, we want to find the slopes and lengths of the sides of a quadrilateral
To find the slopes, we use the equation:
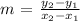
To find the length, we use the equation:
![L\text{ = }\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/sdnwfas4ik6bc6avt365kz861ny25ftmsy.png)
We take the sides one after the other
a) HI
We have the slope as:
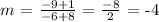
We have the length as:
![\begin{gathered} \sqrt[]{(-6+8)^2(-9+1)^2} \\ =\text{ }\sqrt[]{4+64} \\ =\text{ }\sqrt[]{68} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/b8tf1s555t7cbhx6fdletuchbs4i8koytq.png)
b) IJ
We have the slope as:
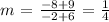
We have the length as:
![\begin{gathered} IJ\text{ = }\sqrt[]{(-6+2)^2+(-8+9)^2} \\ IJ\text{ = }\sqrt[]{17} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vl55sujs86094img9aoi7mposv18jvuj03.png)
c) JK
Slope:

Length:
![\begin{gathered} JK\text{ = }\sqrt[]{2^2+(-8)^2} \\ JK\text{ = }\sqrt[]{68} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/51hmt76eesz7owk2nxh4yjp4c8rhzd02s6.png)
D) KH
Slope:
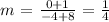
Length:
![\begin{gathered} KH\text{ = }\sqrt[]{(-4+8)^2+(0+1)^2} \\ KH\text{ = }\sqrt[]{17} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zvde6a0hmb8vrmy5ugafedi0alzgdcsp5x.png)
From the answers obtained, the side lengths KH and IJ are the same, while the side lengths JK and KI are the same
Also, looking at the slopes, when the product of the slopes of two lines equal -1, the two lines are perpendicular
Since:

We can conclude that a set of two sides(KH, JK and HI, IJ) are perpendicular
Thus, we have it that the quadrilateral is a rectangle