Question

A 170-foot tall antenna has 4 guy-wires connected to the top of the antenna, and each guy-wire is anchored to the ground. A side-view of this scenario is shown.One of the guy-wires forms an angle of α=0.33 radians with the antenna and the opposing guy-wire forms an angle of β=0.43 radians with the antenna.What is the horizontal distance between anchor 1 and the base of the antenna? ____feet   What is the horizontal distance between anchor 2 and the base of the antenna?_____ feet   What is the distance between anchor 1 and anchor 2? ____feet

Answer 1

Let's label the diagram with the information provided. The diagram would look like:

What is the horizontal distance between anchor 1 and the base of the antenna?

This is labeled as x.

With respect to angle alpha, the side x is opposite and the antenna is the side adjacent.

Thus, we need the trig ratio tan to solve for "x". Shown below:

`\begin{gathered} \tan \alpha=(x)/(170) \\ \tan (0.33)=(x)/(170) \\ x=170*\tan (0.33) \\ x=58.23 \end{gathered}`

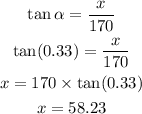
Answer: 58.23 feet

What is the horizontal distance between anchor 2 and the base of the antenna?

This is labeled as y.

With respect to angle beta, the side y is opposite and the antenna is the side adjacent.

Thus, we need the trig ratio tan to solve for "y". Shown below:

`\begin{gathered} \tan \beta=(y)/(170) \\ \tan (0.43)=(y)/(170) \\ y=170*\tan (0.43) \\ y=77.97 \end{gathered}`

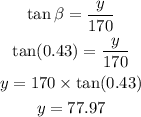
Answer: 77.97 feet

What is the distance between anchor 1 and anchor 2?

The distance between Anchor 1 and Anchor 2 is "x + y". We already found x and y. Let's do the sum:

`\begin{gathered} x+y \\ =58.23+77.97 \\ =136.2 \end{gathered}`

Answer: 136.2 feet