The given expression is
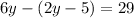
First, we use the distributive property to solve the parenthesis, we have to multiply the negative sign with each term inside the parenthesis.
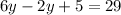
We reduce like terms, 6y and -2y are like terms in this case,
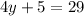
Then, we subtract 5 on each side.
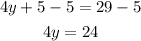
At last, we divide the equation by 4.
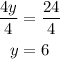
Therefore, the solution is 6.