Question

Given:• PQRS is a rectangle.• mZ1 = 50°PeNSRWhat is mZ2?130°85°70°65°

Answer 1

We can start answering this having that a rectangle is a parallelogram. The diagonals of a parallelogram bisect each other. Therefore, we have that the sides Q to the point where the diagonals intersect each other of the rectangle is congruent to R to this point. Then, we have two congruent sides.

The angles opposite to these sides are congruent too. They have the same measure. Since we have a triangle, and the sum of the internal angles of a triangle is equal to 180, we can say that:

`m\angle1+2\cdot m\angle2=180`

Then, we have:

`50+2\cdot m\angle2=180`

Subtracting 50 from both sides of the equation, and then dividing this equation by 2, we have:

`50-50+2\cdot m\angle2_{}=180-50\Rightarrow2\cdot m\angle2=130`
`2\cdot(m\angle2)/(2)=(130)/(2)\Rightarrow m\angle2=65`

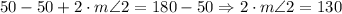
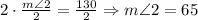
Therefore, the measure of angle 2 (m<2) is equal to 65 (degrees) (last option).