Statement Problem: The sum of two numbers is 7. Five times the larger number plus four times the smaller number is 48. Find the numbers.
Solution:
Let x be the larger number and y be the smaller number such that;

From equation 1, we have;
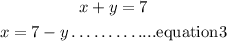
Substitute equation3 in equation2, we have;
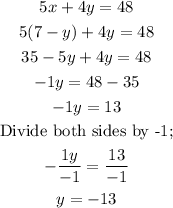
Then, substitute the value of y in equation3;
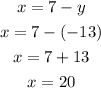
Thus, the larger number is 20 and the smaller number is -13