We start by saying that the deck has 52 cards, in which they have 4 aces (one for each suit).
We are also taking about drawing cards wthout replacement.
Then, for the first draw, we have 4 in 52 chances of drawing an ace.
For the second draw, as one ace is taken out of the deck of cards, there is a chance of 4-1=3 out of 52-1=51 of drawing an ace.
This can be generalized for the 4 draws as:
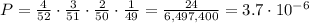
where P is the probability of drawing 4 aces in 4 draws.
There is a probability of 3.7 * 10^(-6) = 0.0000037 = 0.00037% of drawing 4 cards from a standard deck and all 4 being aces.