Question

Use the following information to fill out the entire two-way table.At PRHS, there are 450 students in the 9th and 10th grade taking geometry, and one third ofthem are 9th graders. The students were surveyed on which unit from quarter 4 they liked best.65 students said that unit 5 was their favorite, but only 25 of them were 9th graders. Unit 8 wasthe most popular for 9th graders, with 50 of them saying it was their favorite. Unit 7 was themost popular with 10th graders, with 100 of them saying it was their favorite. Unit 6 and Unit 8were equally popular for 10th grade students. A total of 125 students sald that Unit 6 was theirfavorite.Answer ALL 3 of the following questions.1. What is the probability that a randomly selected student will be a 9th grade student OR astudent that preferred unit 7? Show your work or explain how you know. Leave it insimplified fraction form.2. What is the probability that a randomly selected student will be a 10th grade student whoalso prefers unit 8? Show your work or explain how you know. Leave it in simplifiedfraction form.3. Given the student prefers Unit 5, what is the probability the student is in the 10th grade?Show your work and explain how you know. Leave it in simplified fraction form.

Answer 1

`\begin{gathered} 1)\text{ }(28)/(45) \\ \\ 2)\text{ }(8)/(45) \\ \\ 3)\text{ }(40)/(65) \end{gathered}`

Here, we want to calculate probabilities;

We have this as follows;

1) We want to calculate the probability that a randomly selected student is a 9th grader or a student that preferred unit 7

From here, we need the number of students who are 9th graders and students that prefer unit 7

From the question, we have it that 1/3 of the total students are 9th graders

So, for a total of 450, the number of 9th graders will be 1/3 * 450 = 150 students

Secondly we need the number of students that prefers unit 7

Let us try and complete the table as follows;

From the completed table, the numbers that like unit 7 are 130

So the probability we want to calculate is the sum of the two divided by 450

We have this as;

`(130+150)/(450)\text{ = }(280)/(450)\text{ = }(28)/(45)`

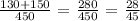
2) Here, we want to calculate the probability that a randomly selected student is a 10th grader who also prefers unit 8

From the table, we can see that the number of students who are 10th graders and also prefer unit 8 is 80

So, we have the probability as;

`(80)/(450)\text{ = }(8)/(45)`

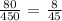
3) Here, we want to calculate the probability that given that a student prefers unit 5, what is the probability that he is a 10th grader

We use the conditional probability value here

Where event A is the probability that student is a 10th grader, while event B is the probability that a student prefers unit 5

We have the probability as;

`\begin{gathered} P(A|B)\text{ = }(P(AnB))/(P(B)) \\ \\ P(\text{AnB) = }(40)/(450);\text{ P(B) = }(65)/(450) \\ \\ P(A|B)\text{ = }(40)/(65) \end{gathered}`